(Based on inputs from Ulrike Feudel )
It is common for non-linear systems to be multi stable, this is, the systems has multiple potential stable states. The potential in different system states can be used to define a stability landscape. The sections of a stability landscape that attract the system are called basins of attraction, which can be used to define the system stable states.
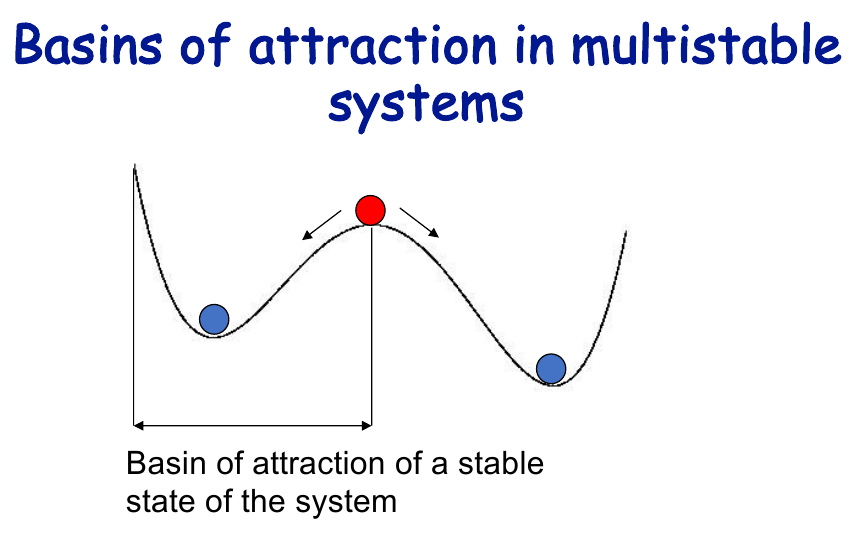
Considering multi stable systems, lets have a look at a new definition of resilience:
“The Ability of systems to react on long-term changes of external conditions or perturbations in such a way, that a sustainable development of the society becomes possible without break-downs corresponding to undesired alternative states”.
Which properties make a system resilient with respect to perturbations? Can Resilience be Measured?
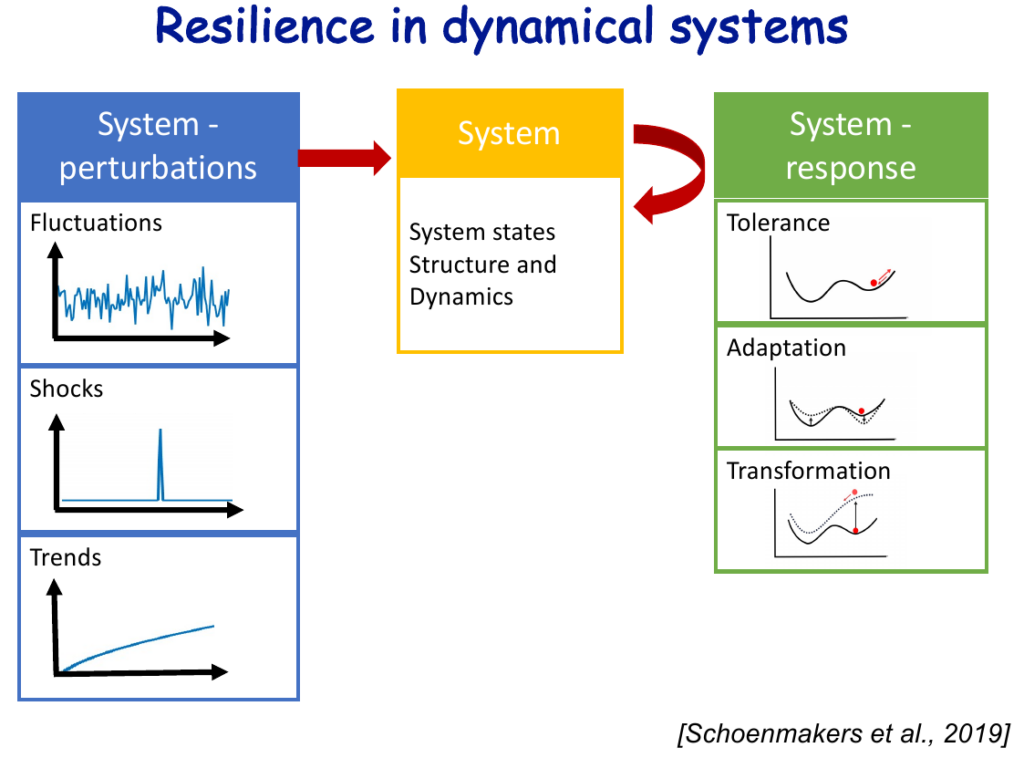
According to the kind of perturbations, different indicators can aid us to explore (measure) a system resilience, towards the specific perturbation. Some examples are:
- for small perturbations -> recovery rate
- for large perturbations – > smallest perturbation which is necessary to leave the current system state.
- for noisy systems -> mean scape time.
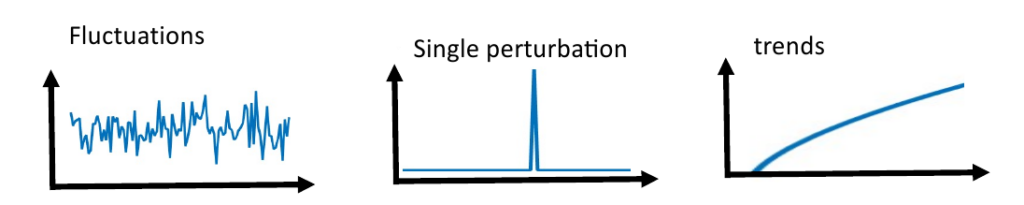
How does transitions between alternative stable states take place? Which disturbances lead to a transition to an alternative stable state (or regime shift)?
Systems react different to each type of perturbation that can create trigger or tipping mechanisms:
- B-tipping: abrupt changes in the dynamics (bifurcation) when parameters cross critical thresholds. The perturbation is very slow regarding the time scale of internal dynamics. e.g. climate change, hydrographic conditions.
- N-tipping: Noise in the system that can create jump between different stable states.
- S-tipping: Shock or extreme event tipping, in which the perturbation is so large that the system crosses immediately the boundary of the basin of attraction.
- R-tipping: Rate-induced tipping, where parameters change faster than the system can track its stable state. Depends on threshold in the speed of change. e.g. change in nutrient conditions in a lake.
More over, in dynamical systems, where stability landscapes are not constant, tolerance, adaptation and transformation play an important role in system resilience.